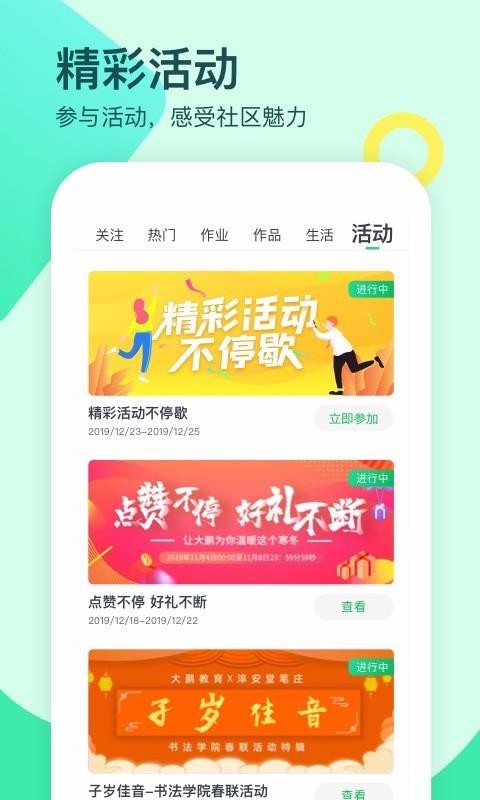
教育质量评价-评价质量教育的标准

研究生姓名：**** 课程编号：2111308053 专业：教育管理 研究生所在学院：教育学院 课程任课教师姓名：**** 成绩(占比)： 课程名称：教育质量评估专题成绩 任课教师签名： 多元智能教学设计——双曲线的几何性质 学科 双曲线的几何性质 学科 数学 第三学期 年级 高中 教学背景分析 教学内容分析：本节内容属于解析几何的范畴，解析几何的基本方法是结合代数来学习，即通过方程的分析来研究双曲线的性质。在本节之前已经学过椭圆的几何性质，学生通过类比的方式，探究双曲线的几何性质应该不难。 学生情况分析：我校是广州市国家级示范性高中，但是学校的生源并不是特别好，对老师传授的知识不够重视吸收，对老师传授的内容缺乏主动质疑和发展。 发现问题、提出问题的能力比较弱，在数学思维的深度和广度上还有一定的欠缺。 教学方法与手段：本课根据教学内容的特点和学生的实际情况，通过学生的自我探索、讨论，在教师的指导下，采用探索、合作交流的方式，引导学生对探索过程中的某些环节提出问题，产生小课题，供课后进一步研究探索，将探索活动延伸到课后更广阔的舞台。 技术准备： 硬件：电脑、实物投影仪； 软件：ppt、几何画板 教学目标 教学目标 1.理解双曲线的范围、对称轴、顶点、实轴、虚轴、渐近线等概念，知道它们描述了双曲线的哪些几何性质。

2、在探究双曲线几何性质的过程中，学生将体验到用数论方法形成的一般方法：曲线方程——分析得到代数性质——对应到曲线的几何性质，促进学生对“数”与“形”之间联系的应用与理解。 3、鼓励学生在学习中敢于质疑、深入思考、积极探索，让学生体验到数学发现和知识发展的过程，享受在思维进步中不断获得新发现的乐趣，培养学生的创新意识和能力，树立正确的数学学习观。 4、通过教师的讲解与分析，引导学生对无穷大有一定的认识，并尝试用无穷大的思想从方程的角度解释双曲线具有渐近性质的原因。 教学重点： 1、双曲线的几何性质：值域、对称性、顶点、实轴、虚轴、渐近线。 2、进一步理解、运用、体会从代数角度研究几何的思想和方法。教学难点：感性接受虚轴、发现与认识渐近线 多种智能类别 语言智能 汇编智能 空间智能 动态智能 音乐智能 人际智能 内省智能 回顾椭圆的几何性质 分析椭圆几何性质的由来 小组讨论 通过类比推理得到双曲线的几何性质，各小组画出交流共同协商教学过程图示 清晰列出双曲线的几何性质 4、各小组派代表汇报小组成果 展示各小组表格，让各小组在老师的指导下进行比较，总结出正确的性质 学生学习效果评估 设计 评估方式 评估内容 评估项目 评估水平 学生参加小组活动的积极性 学生类比推理能力 课上独立思考能力 学生口头表达能力 对其他小组的结论、意见提出质疑、批评的能力 将所学内容迁移的能力 学生主动提前复习 独立学习的愿望探索 独立思考的习惯 参与小组交流 积极参与课堂